Зачем знать теорему Виета — применение в реальной жизни и математике

Теорема Виета из алгебры - это одна из основных теорем, которые имеют огромное значение в реальной жизни.

Она названа в честь французского математика Франсуа Виета, который в 16 веке разработал эту теорему. Теорема Виета связывает корни алгебраического уравнения с его коэффициентами. Она даёт нам возможность вычислить сумму корней и их произведение, даже не зная самих корней.

Теорема Виета находит применение в различных областях науки и техники. Например, она используется в физике для решения задач, связанных с движением тела. Математики применяют её при поиске корней сложных уравнений, что важно для решения многих практических задач.

Также теорема Виета находит применение в финансовой математике. Коэффициенты алгебраического уравнения могут представлять собой ставки по кредитам, доходы или затраты компании. Теорема Виета позволяет определить различные финансовые показатели, такие как сумма или произведение доходов или затрат.

Таким образом, теорема Виета имеет широкое применение в решении практических задач, связанных с физикой, математикой, финансами и другими областями науки и техники. Она помогает нам лучше понять и исследовать мир, в котором мы живём, и применить полученные знания в реальной жизни.

Как теорема Виета помогает в жизни?

Несмотря на то, что теорема Виета изначально разработана для решения математических задач, она находит применение и в реальной жизни. Ее простота и универсальность позволяют использовать ее для решения различных задач и проблем.

Одним из применений теоремы Виета является нахождение корней уравнений. Если у вас есть квадратное уравнение, требующее для решения нахождения корней, вы можете использовать теорему Виета для определения этих корней. Метод Виета позволяет найти сумму и произведение корней уравнения на основе его коэффициентов. Это упрощает процесс нахождения корней и может сэкономить время и усилия.

Другим применением теоремы Виета является нахождение коэффициентов многочлена. Если даны корни многочлена, теорема Виета позволяет найти его коэффициенты. Это может быть полезно при построении графика многочлена или анализе его свойств. Например, если у вас есть квадратное уравнение и вы знаете его корни, теорема Виета позволяет найти коэффициенты этого уравнения и использовать их для построения графика.

Теорема Виета также может быть полезна при работе с симметричными многочленами. Она позволяет устанавливать связь между коэффициентами симметричного многочлена и его корнями. Это может быть полезно при решении задач на определение симметричного многочлена по его коэффициентам или нахождение коэффициентов симметричного многочлена на основе его корней.

В целом, теорема Виета является мощным инструментом, который помогает в решении различных математических проблем и задач как в школе, так и в реальной жизни. Благодаря ей, мы можем упростить и ускорить процесс нахождения корней уравнений, анализа свойств многочленов и решения других задач, связанных с многочленами и их корнями.

Анализ корней уравнений

Теорема Виета позволяет нам не только находить корни уравнений, но и проводить анализ этих корней для получения дополнительной информации о решении уравнения. Рассмотрим несколько примеров практического применения этой теоремы.

1. Определение суммы и произведения корней. Используя теорему Виета, мы можем выразить сумму и произведение корней уравнения через коэффициенты этого уравнения. Эта информация может быть очень полезна, например, при решении задач из физики, где требуется вычислить значения корней и их сумму или произведение.

3. Связь между корнями и коэффициентами. Теорема Виета позволяет установить связь между корнями уравнения и его коэффициентами. Например, сумма кубических корней полностью соответствует отношению коэффициента перед старшей степенью в уравнении. Это позволяет нам понять, как изменение коэффициентов влияет на корни уравнения и наоборот.

Таким образом, анализ корней уравнений с использованием теоремы Виета может быть полезным инструментом при решении различных задач, связанных с поиском и изучением корней уравнений.

Решение квадратных уравнений

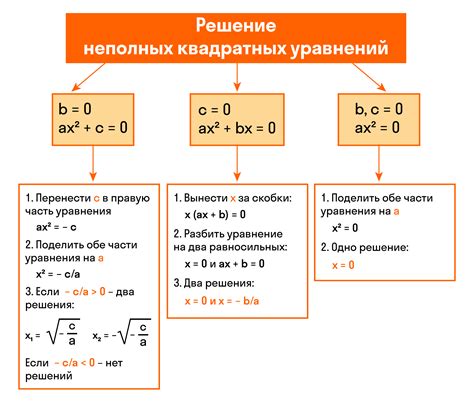
Согласно теореме Виета, сумма корней квадратного уравнения равна отрицательному коэффициенту b, деленному на коэффициент a. Также произведение корней равно коэффициенту c, деленному на a. Эти формулы позволяют быстро и легко найти значения корней квадратного уравнения, необходимые в реальной жизни.

Рассмотрим пример. Пусть у нас есть квадратное уравнение x^2 - 5x + 6 = 0. С помощью теоремы Виета мы можем найти сумму корней и их произведение. Здесь a = 1, b = -5 и c = 6. Согласно теореме Виета:

Сумма корней = -b/a = -(-5)/1 = 5

Произведение корней = c/a = 6/1 = 6

Таким образом, мы узнали, что сумма корней данного уравнения равна 5, а их произведение равно 6.

Это может быть полезно, например, при решении задач, связанных с физикой или экономикой. Решая такие уравнения, мы можем найти значения переменных, которые представляют собой реальные физические величины или экономические показатели.

Определение коэффициентов уравнений

Коэффициент a - это коэффициент при x² и влияет на ветви параболы, определяя ее направление и степень открытости. Если коэффициент a положителен, то парабола открывается вверх, а если отрицателен - вниз.

Коэффициент b - это коэффициент при x и определяет, где находится вершина параболы. В случае, если коэффициент b равен нулю, то вершина находится на оси y.

Коэффициент c - это свободный член уравнения и определяет точку, где парабола пересекает ось y.

Теорема Виета позволяет связать коэффициенты уравнения и корни этого уравнения. В частности, она устанавливает, что сумма корней уравнения равна противоположному знаку коэффициента b, а произведение корней равно коэффициенту c, поделенному на коэффициент a.

Таким образом, теорема Виета позволяет использовать коэффициенты уравнения для определения свойств и характеристик этого уравнения. Она находит свое применение в различных областях, таких как алгебра, физика и экономика, и помогает решить разнообразные практические задачи.

Применение в финансовых расчетах

Теорема Виета, которая изначально была разработана для решения алгебраических уравнений, также находит свое применение в финансовых расчетах. Эта теорема позволяет нам вычислять корни уравнений через сумму и произведение его коэффициентов.

В контексте финансовых расчетов, теорема Виета может быть использована для определения значений переменных в уравнениях, связанных с финансовыми инструментами, такими как акции, облигации или процентные ставки.

Одним из основных примеров применения теоремы Виета в финансах является расчет скидок и наценок. Например, представим себе ситуацию, когда новая модель автомобиля продается с определенной скидкой. Эта скидка может быть представлена как значение переменной в уравнении, связанном с ценой автомобиля. Используя теорему Виета, можно определить значение цены автомобиля, зная сумму и произведение его коэффициентов.

Еще одним примером применения теоремы Виета в финансовых расчетах является расчет процентной ставки по кредиту или депозиту. Предположим, что мы знаем сумму вклада и общую сумму вклада без процентов. Мы также знаем, что процентная ставка и срок вклада являются неизвестными значениями. Применение теоремы Виета позволяет нам определить значения процентной ставки и срока вклада, если мы знаем сумму и произведение соответствующих коэффициентов.

Таким образом, теорема Виета имеет широкое применение в финансовых расчетах, позволяя определить значения переменных в уравнениях, связанных с финансовыми инструментами и операциями, такими как расчет скидок и наценок, процентных ставок по кредиту или депозиту, и других финансовых параметров.

Прогнозирование экономических показателей

Теорема Виета имеет широкое применение в прогнозировании экономических показателей. Экономические модели, которые основаны на теореме Виета, позволяют предсказывать будущую динамику различных экономических показателей, таких как инфляция, безработица, ВВП и другие.

В основе прогнозирования лежит анализ корней квадратного уравнения, которое смоделировано на основе исторических данных. Известно, что корни квадратного уравнения, выражающиеся через коэффициенты этого уравнения (либо через их сумму, либо через их произведение), содержат информацию о динамике и характеристиках экономической системы.

Также теорема Виета используется для определения точек перегиба в экономической системе. Эти точки могут указывать на критические моменты, связанные с изменением траектории экономического роста или снижением устойчивости экономической системы. Предсказание и анализ таких точек перегиба является важным инструментом для принятия экономических решений и планирования бизнес-стратегий.

Таким образом, использование теоремы Виета в прогнозировании экономических показателей позволяет дать количественную оценку и представление о прошлых и будущих изменениях в экономической сфере. Это помогает экономистам и аналитикам принимать осознанные решения и строить эффективные стратегии для достижения экономического роста и стабильности.

Решение задач геометрии

Теорема Виета, изначально разработанная для решения квадратных уравнений, может быть применена и в геометрии для решения некоторых задач. Это особенно полезно в ситуациях, когда нужно найти значения сторон или углов в геометрической фигуре на основе их суммы или произведения.

Например, рассмотрим задачу о треугольнике. Пусть известны значения двух сторон треугольника и сумма всех трех сторон. С помощью теоремы Виета мы можем найти значение третьей стороны. Зная, что сумма всех трех сторон треугольника равна A + B + C, где A, B, C - значения сторон, мы можем записать уравнение:

A + B + C = сумма сторон

Предположим, что известны значения A и B, а также сумма сторон треугольника. Тогда, зная два из трех значений, мы можем с использованием теоремы Виета вычислить третье значение:

C = сумма сторон - (A + B)

Таким же образом, теорема Виета может быть применена для решения других задач геометрии, где известны суммы или произведения значений сторон или углов. Это может быть полезно, например, при нахождении неизвестных значений углов в многоугольнике или нахождении неизвестных значений сторон в прямоугольнике или круге.

Таким образом, теорема Виета является мощным инструментом для решения задач геометрии, позволяя находить неизвестные значения сторон и углов на основе известных сумм или произведений. Это делает ее полезной для решения практических задач в различных областях, где геометрия играет важную роль, например, в инженерии, архитектуре или строительстве.

Применение в физических расчетах

Теорема Виета, изначально применявшаяся в алгебре для решения квадратных уравнений, также может быть использована в физических расчетах для нахождения корней уравнений, связанных с физическими процессами и явлениями.

Одним из примеров может служить расчет движения тела под действием силы тяжести. Пусть у нас есть тело массой m, которое брошено вертикально вверх с начальной скоростью v. Нам нужно найти максимальную высоту, на которую поднимется тело.

Используем уравнение движения тела в вертикальной плоскости:

h(t) = v₀t - (g/2)t²,

где h(t) - высота тела в момент времени t, v₀ - начальная скорость, g - ускорение свободного падения.

Максимальная высота достигается в тот момент времени, когда вертикальная скорость становится равной нулю, то есть v(t) = 0.

Подставим это условие в уравнение движения и решим полученное квадратное уравнение:

0 = v₀t - (g/2)t²,

0 = gt² - 2v₀t.

Применяя теорему Виета, мы можем найти корни этого уравнения. Учитывая, что первый коэффициент равен g, а второй -2v₀, можем записать:

t₁ + t₂ = -(-2v₀/g) = 2v₀/g

Таким образом, мы найдем сумму корней уравнения, которая равна времени полета тела.

Зная время полета, мы можем найти максимальную высоту подстановкой этого значения в начальное уравнение:

h(t) = v₀(2v₀/g) - (g/2)(2v₀/g)²,

h(t) = (v₀)²/g - (v₀)²/2g,

h(t) = (v₀)²/2g.

Таким образом, теорема Виета позволяет нам найти максимальную высоту подъема тела, брошенного вертикально вверх, используя значения начальной скорости и ускорения свободного падения.

Анализ оптимального решения задач

Математические модели позволяют описать задачу в виде формальной математической структуры. Они учитывают все параметры и факторы, которые влияют на решение задачи. Важным инструментом при анализе оптимального решения задач являются теоремы и алгоритмы, которые позволяют находить наилучшие решения.

Для анализа оптимального решения задач обычно используются различные методы, такие как методы оптимизации, линейного программирования, теории игр и др. Они позволяют найти оптимальное решение при заданных условиях, минимизировать затраты и максимизировать выгоду.

Анализ оптимального решения задач необходим при принятии решений в различных сферах деятельности. Например, при планировании производства, распределении ресурсов, организации логистики, управлении финансами и др.

Использование математических моделей и методов позволяет сделать решение более обоснованным и эффективным. Анализ оптимального решения задач помогает рационально использовать доступные ресурсы, уменьшить затраты и повысить эффективность деятельности.