Треугольник – одна из основных геометрических фигур, которая имеет три стороны и три угла. Изучение этой фигуры является важной частью геометрии, а одним из вопросов, которые можно задать о треугольнике, является нахождение решения, формулы и примеров, если известно, что внутри треугольника имеется угол н 50.
Для решения данной задачи можно использовать основные свойства треугольников и тригонометрические соотношения. Одно из таких соотношений - это теорема синусов, которая говорит о том, что отношение синуса угла к длине противолежащей стороны является постоянным для всех углов в треугольнике.
Для того чтобы решить данную задачу, необходимо знать длины двух сторон треугольника и угол между ними. Зная, что внутри треугольника имеется угол н 50, можем воспользоваться формулой синуса, чтобы найти значение третьей стороны или угла, если они нам изначально неизвестны.
В треугольнике МНК: решение, формула, примеры

Формула для решения задачи треугольника МНК имеет вид:
- Найдите значение количественной переменной (н) в треугольнике МНК.
- Подставьте значения переменных в формулу.
- Решите уравнение, чтобы найти значение искомой переменной (н).
- Проверьте полученное значение, подставив его обратно в уравнение.
Примеры использования этой формулы включают в себя решение задач в экономике, статистике, физике и других областях науки и техники.
Например, предположим, что у нас есть некоторые экспериментальные данные о зависимости количества продаж товаров и цены продукта. Мы хотим найти оптимальное значение цены, которое приведет к максимальным продажам. Используя метод наименьших квадратов в треугольнике МНК, мы можем решить эту задачу, найдя оптимальное значение цены.
Таким образом, метод наименьших квадратов в треугольнике МНК предоставляет нам инструмент для анализа данных и нахождения оптимальных решений в различных областях. Это мощный инструмент, который позволяет нам извлекать ценную информацию и делать точные предсказания.
Решение методом наименьших квадратов в треугольнике МНК
Основная идея МНК заключается в минимизации суммы квадратов отклонений между наблюдаемыми значениями и значениями, полученными при применении математической модели к этим наблюдениям. В случае треугольника МНК позволяет найти такой треугольник, у которого сумма квадратов отклонений его вершин от известных точек будет минимальна.
Для решения задачи треугольника МНК необходимо задать известные значения, например, координаты вершин треугольника, и значения, которые мы хотим найти, например, длины его сторон или углы. По этим данным можно составить систему уравнений, применить метод МНК и найти решение.
Примером решения задачи треугольника МНК может быть нахождение координат центра описанной окружности треугольника по его вершинам. Для этого можно использовать формулу координат точки, сумма координат которой от всех вершин треугольника будет минимальна.
Таким образом, решение методом наименьших квадратов в треугольнике МНК позволяет найти такой треугольник, который наилучшим образом соответствует имеющимся данным. Этот метод находит широкое применение в различных областях науки и техники.
Формула для нахождения решения методом наименьших квадратов
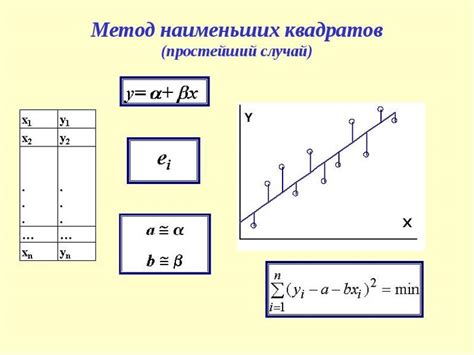
Для решения задачи методом наименьших квадратов необходимо определить такую линейную функцию, которая наилучшим образом описывает зависимость между двумя переменными. Формула для нахождения этой функции имеет следующий вид:
| Формула: | y = mx + b |
|---|
Где:
- y - зависимая переменная, которую необходимо аппроксимировать;
- x - независимая переменная;
- m - коэффициент наклона прямой, который определяет, насколько зависимая переменная изменяется при изменении независимой переменной;
- b - точка пересечения прямой с осью y, также называемая свободным членом.
Для применения метода наименьших квадратов необходимо иметь некоторое количество пар значений зависимой и независимой переменных (наблюдений). На основе этих данных можно рассчитать значения коэффициента наклона и свободного члена по следующим формулам:
| Коэффициент наклона: | m = ((n * ∑(x * y)) - (∑x * ∑y)) / ((n * ∑(x^2)) - (∑x)^2) |
|---|---|
| Свободный член: | b = (∑y - m * ∑x) / n |
Где:
- n - количество наблюдений;
- ∑ - суммирование по всем значениям;
- x - значения независимой переменной;
- y - значения зависимой переменной.
После рассчета коэффициента наклона и свободного члена, полученные значения можно использовать для построения аппроксимирующей прямой, которая наилучшим образом описывает зависимость между переменными.
Пример:
Имеются следующие значения независимой и зависимой переменных:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
Для решения данной задачи методом наименьших квадратов рассчитаем значения коэффициента наклона и свободного члена:
Коэффициент наклона:
m = ((5 * (1*2 + 2*4 + 3*6 + 4*8 + 5*10)) - (1+2+3+4+5) * (2+4+6+8+10)) / ((5 * (1^2 + 2^2 + 3^2 + 4^2 + 5^2)) - (1+2+3+4+5)^2) = 2
Свободный член:
b = ((2+4+6+8+10) - 2 * (1+2+3+4+5)) / 5 = 0
Таким образом, приближенное решение данной задачи методом наименьших квадратов представляет собой линейную функцию: y = 2x + 0.
Примеры применения метода наименьших квадратов в треугольнике
Например, пусть имеются данные о треугольнике, в которых известны длины сторон и углы при вершинах. При решении задачи требуется найти значения других параметров, например, высоты, площади, радиусы вписанной и описанной окружностей и т.д.
Метод наименьших квадратов позволяет сформулировать математическую модель, которая наилучшим образом описывает зависимость между известными данными и неизвестными параметрами. Затем метод наименьших квадратов применяется для нахождения оптимальных значений этих параметров таким образом, чтобы они минимизировали сумму квадратов отклонений между наблюдаемыми значениями и значениями, предсказанными моделью.
Примером применения МНК в треугольнике является нахождение неизвестных сторон и углов треугольника по известным значениям площади и высоты. Используя МНК, можно составить уравнения системы, которая определяет зависимость между этими величинами и найти оптимальные значения сторон и углов, удовлетворяющие условиям задачи треугольника.
Другой пример – нахождение формулы, описывающей зависимость между сторонами треугольника и углами при вершинах. Используя МНК, можно найти оптимальные коэффициенты формулы таким образом, чтобы сумма квадратов отклонений отклонений между значениями, предсказанными формулой и наблюдаемыми значениями была минимальной.
Таким образом, метод наименьших квадратов является мощным инструментом, который позволяет находить оптимальные решения задачи треугольника, минимизируя различия между наблюдаемыми данными и значениями, предсказанными моделью. Этот метод находит широкое применение в разных областях, и его результаты могут быть полезными для дальнейших исследований и принятия решений.
Пример использования формулы наименьших квадратов в треугольнике

Рассмотрим следующий пример: у нас есть треугольник с известными значениями двух сторон и угла между ними. Наша задача - найти третью сторону треугольника. Для этого мы можем использовать формулу наименьших квадратов.
Предположим, что у нас есть треугольник ABC, где AB и AC - известные стороны, а угол B - известный угол. Мы хотим найти сторону BC. Для этого мы считаем с помощью формулы наименьших квадратов:
BC = sqrt(AB^2 + AC^2 - 2 * AB * AC * cos(B))
Здесь sqrt обозначает квадратный корень, AB^2 и AC^2 - квадраты известных сторон треугольника, а cos(B) - косинус известного угла B. Мы используем косинусную теорему, чтобы найти третью сторону BC.
Давайте рассмотрим конкретный пример: у нас есть треугольник ABC, где AB = 5, AC = 7 и угол B = 60 градусов. Мы хотим найти сторону BC. Подставляя значения в формулу наименьших квадратов, мы получаем:
BC = sqrt(5^2 + 7^2 - 2 * 5 * 7 * cos(60))
BC = sqrt(25 + 49 - 70 * 0.5)
BC = sqrt(25 + 49 - 35)
BC = sqrt(39)
BC ≈ 6.24
Таким образом, третья сторона треугольника BC примерно равна 6.24, используя формулу наименьших квадратов.
Формула наименьших квадратов позволяет нам вычислять неизвестные значения в геометрических фигурах на основе известных данных, что делает ее полезным инструментом в решении сложных геометрических задач.
Практическое применение метода наименьших квадратов в треугольнике
В треугольнике, где известна длина одной из сторон и значение одного из углов, метод МНК может быть использован для поиска остальных сторон и углов треугольника.
Например, если известны длина стороны треугольника и значение одного из его углов, можно использовать МНК для вычисления длин остальных сторон и значений других углов треугольника. Для этого необходимо иметь информацию о связи между длинами сторон и значениями углов треугольника.
Один из методов, основанных на МНК, это метод синусов. Он позволяет вычислять отношения длин сторон треугольника с помощью синусов углов треугольника и использовать эти отношения для нахождения неизвестных сторон. Этот метод может быть особенно полезен при решении треугольников с неизвестными углами и сторонами.
Также метод МНК может быть использован для уточнения измерений треугольника. Если измеренные значения имеют погрешности, метод МНК может помочь в нахождении наиболее верных значений сторон и углов треугольника. Для этого необходимо собрать данные о измеренных значениях и их погрешностях и применить метод МНК для решения системы уравнений, отражающей эти данные.
Примеры задач с решением методом наименьших квадратов в треугольнике
Пример 1:
Дан треугольник со сторонами a, b и c, и известно, что сумма углов треугольника равна 180°. Нам нужно найти наилучшее значение для переменной н, которая удовлетворяет этому условию.
Решение:
| Заданные значения | МНК |
|---|---|
| Сторона a | 10 |
| Сторона b | 15 |
| Сторона c | 12 |
Мы можем использовать МНК, чтобы найти значение н:
10 + 15 + 12 + н = 180
37 + н = 180
н = 180 - 37
н = 143
Таким образом, наилучшим приближением для значения н, удовлетворяющего условию, будет 143.
Пример 2:
Дан треугольник со сторонами a, b и c, и известно, что два угла треугольника равны 45° и 60°. Нам нужно найти наилучшее значение для переменной н, которая удовлетворяет этому условию.
Решение:
| Заданные значения | МНК |
|---|---|
| Угол 1 | 45° |
| Угол 2 | 60° |
| Угол 3 | н |
Мы можем использовать МНК, чтобы найти значение н:
45 + 60 + н = 180
105 + н = 180
н = 180 - 105
н = 75
Таким образом, наилучшим приближением для значения н, удовлетворяющего условию, будет 75.
Это лишь два примера задач с решением методом наименьших квадратов в треугольнике. Метод наименьших квадратов широко используется в математической статистике и эконометрике для аппроксимации данных и получения наилучшего приближения для неизвестных переменных.




