Понятие предела функции является одним из фундаментальных в математике. Особенно важным является понятие предела функции при х стремящемся к 0. В этой статье мы рассмотрим основные понятия и методы расчета предела функции при таком условии.
Предел функции f(x) при х стремящемся к 0 обозначается lim(x→0)f(x) и определяется следующим образом: если для произвольного положительного числа ε существует такое число δ, что для всех x из проколотой окрестности (0, δ) выполняется неравенство |f(x) - L|
Основные методы расчета пределов функций при х стремящемся к 0 включают использование арифметических свойств пределов, замечательных пределов, а также правила Лопиталя. Арифметические свойства пределов позволяют переходить от сложных функций к более простым, используя операции сложения, вычитания, умножения и деления. Замечательные пределы являются частным случаем арифметических свойств и позволяют легко вычислять пределы для некоторых элементарных функций. Правило Лопиталя применяется для вычисления пределов неопределенностей вида 0/0, ∞/∞ и ∞ - ∞.
Основные понятия и методы расчета предела х при х стремящемся к 0
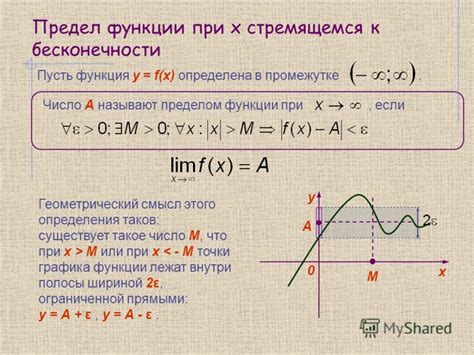
Для того чтобы вычислить предел х при х стремящемся к 0, необходимо использовать различные методы расчета. В основе этих методов лежит понятие "предела функции".
Предел функции - это значение, к которому стремится функция при приближении аргумента к определенной точке. Если приближение к точке происходит с разных направлений и значения пределов с обоих сторон равны между собой, то говорят о существовании предела функции в данной точке.
Расчет предела х при х стремящемся к 0 можно производить с помощью различных методов, таких как:
- Аналитический метод - основан на использовании алгебраических преобразований и свойств функций. С помощью аналитического метода можно найти асимптотическое приближение функции и вычислить предел.
- Геометрический метод - позволяет записать функцию в виде графической зависимости и использовать ее свойства для вычисления предела.
- Численный метод - основан на приближенном вычислении значений функции вблизи точки и проверке полученных результатов на монотонность и сходимость.
Расчет предела х при х стремящемся к 0 является важным шагом при изучении математического анализа и применяется во множестве задач и заданий. Понимание основных понятий и методов расчета предела позволяет более глубоко изучать функции и их свойства.
Сущность предела и его определение
Определение предела функции дается через окрестности точки и ее приближение к ней. Для функции f(x) существование предела в точке x = a означает, что при приближении значения x к a, значения самой функции f(x) стремятся к некоторому числу L.
Формально, говорят, что предел функции f(x) при x стремящемся к a равен числу L, если для любого положительного числа ε существует положительное число δ, такое что для всех x, для которых 0
В данном определении a называется точкой сходится предела, а L – конечным числом, к которому стремится функция. Он может быть любым числом – как положительным, так и отрицательным, или нулем.
Теоремы о пределе функции

При изучении пределов функций очень важно понимать, как применять различные теоремы, которые помогут упростить расчеты и получить более точный результат.
Одной из базовых теорем является теорема о пределе суммы функций. Согласно этой теореме, если исходные функции имеют пределы при данном значении аргумента, то предел их суммы будет равен сумме их пределов.
Другой важной теоремой является теорема о пределе произведения функций. Если исходные функции имеют пределы, то предел их произведения равен произведению их пределов.
Также существует теорема о пределе частного функций. Если исходные функции имеют пределы, то предел их частного будет равен частному их пределов, при условии, что знаменатель не равен нулю.
Обратная теорема о пределе функции связывает ограниченность функции и ее предел. Если функция ограничена на некотором интервале и имеет предел на этом интервале, то предел функции будет равен ее наибольшему предельному значению на этом интервале.
Эти теоремы помогают упростить расчеты и дать более точный ответ при нахождении предела функции.
Использование предела для нахождения производной
Для нахождения производной функции f(x) в точке x=a можно воспользоваться формулой:
f'(a) = limx→a (f(x) - f(a)) / (x - a)
То есть, производная в точке a равна пределу отношения изменения функции f(x) к изменению ее аргумента x при стремлении x к a.
Используя данную формулу, можно найти производную любой функции при условии, что предел существует.
Пример решения задачи на нахождение производной с помощью предела:
Дана функция f(x) = 3x2 + 2x - 1. Найдем производную функции в точке x=2.
f'(2) = limx→2 (f(x) - f(2)) / (x - 2)
Подставляем значение функции и точки в формулу производной:
f'(2) = limx→2 ((3x2 + 2x - 1) - (3*22 + 2*2 - 1)) / (x - 2)
f'(2) = limx→2 (3x2 + 2x - 1 - 16) / (x - 2)
f'(2) = limx→2 (3x2 + 2x - 17) / (x - 2)
Упрощаем числитель:
f'(2) = limx→2 (3(x - 1)(x - 2)) / (x - 2)
Сокращаем похожие слагаемые и получаем:
f'(2) = limx→2 3(x - 1) = 3(2 - 1) = 3
Таким образом, производная функции f(x) = 3x2 + 2x - 1 в точке x=2 равна 3.
Таким образом, использование предела позволяет найти производную функции в точке и определить ее скорость изменения в этой точке.
Методы расчета предела: подстановка, стандартные пределы

Применение метода подстановки может быть полезно, например, в случае с пределами вида lim f(x), при x → a, где функция f(x) неопределена в точке a. В таких случаях можно рассмотреть другой предел:
lim f(g(x)), при x → a, где g(x) определена в точке a.
Метод подстановки позволяет упростить вычисление предела, заменив сложное выражение на простое.
Еще один способ расчета пределов – использование стандартных пределов. Стандартные пределы это пределы, которые уже вычислены и известны. Некоторые из них приведены в таблице:
- Предел синуса: lim sin(x) = 0, при x → 0.
- Предел косинуса: lim cos(x) = 1, при x → 0.
- Предел экспоненты: lim e^x = e, при x → 0.
- Предел натурального логарифма: lim ln(x) = -∞, при x → 0.
- Предел обратной функции: lim 1/x = ∞, при x → 0.
Используя стандартные пределы, можно свести вычисление сложных пределов к более простым выражениям.
Вычисление предела при помощи замечательных пределов
Наиболее часто используемые замечательные пределы:
| Предел | Значение |
|---|---|
| limx→0 (sin x)/x | 1 |
| limx→0 (1-cos x)/x | 0 |
| limx→0 (1+x)1/x | e |
Для вычисления предела функции, содержащей одну из этих функций в числителе или знаменателе, можно использовать соответствующий замечательный предел. Например, если необходимо вычислить предел функции limx→0 (sin 3x)/(2x), можно воспользоваться замечательным пределом для limx→0 (sin x)/x, получив значение 3/2.
Помимо этих замечательных пределов, существуют и другие полезные тождества и свойства пределов, которые также могут быть использованы для облегчения вычислений. Важно помнить, что данные пределы справедливы только в тех случаях, когда исходная функция обладает заданными условиями существования предела.
Таким образом, использование замечательных пределов является мощным инструментом при вычислении пределов функций и позволяет значительно упростить и ускорить данную задачу.
Применение предела при решении задач на определение производной

Предположим, у нас есть функция f(x), и мы хотим найти ее производную в точке x = a. Мы можем воспользоваться определением производной через предел:
f'(a) = lim(x → a) ((f(x) - f(a)) / (x - a))
Для этого мы стремим x к a и анализируем поведение функции в этой точке. Если предел этого выражения существует, то он и будет значением производной функции в точке a.
Предел х при х стремящемся к 0 позволяет нам приблизиться к точке a, не достигая ее, и исследовать мгновенное изменение функции в этой точке. Использование этого метода упрощает расчет производной и позволяет решать более сложные задачи, например, нахождение производной сложной функции или функции, заданной параметрически.
Применение предела при решении задач на определение производной позволяет нам понять, как функция меняется в каждой точке и находить точки экстремума, точки перегиба и другие важные характеристики функции. Это важный инструмент для изучения и анализа функций и позволяет нам понять их поведение на уровне отдельных точек и в целом.




