e - основание натурального логарифма, π - математическая константа - число "пи", i - мнимая единица. Казалось бы, что может быть общего между ними? Но именно такое выражение e в степени π i равно 1. Это феноменальное равенство, которое поражает умы и удивляет с самого давних времен.
Для понимания этой загадки необходимо ознакомиться с основами теории комплексных чисел и разложения числа e в степенной ряд. Мнимая единица, обозначаемая i, обладает удивительным свойством: i в кубе равняется -1, а i в четвертой степени равняется 1. Она открывает перед нами новую математическую реальность, в которой мы можем смешивать и действовать одновременно с действительными и мнимыми числами.
Теперь вернемся к выражению e в степени π i. Если выполнять разложение числа e в степенной ряд, можно увидеть, что его можно записать как сумму всех натуральных степеней, равных 1/0!, 1/1!, 1/2!, 1/3! и так далее. Аргументом степени может быть любое число, в том числе и мнимое. Заметим, что когда мы подставляем π i в это выражение, все члены ряда будут иметь вид 1/0!, 1/π! i, 1/2π! i^2 и так далее. Очевидно, что все члены ряда с нечетными показателями степеней будут равны нулю. И только члены с четными показателями степеней дадут нам ненулевые значения.
Изучение постоянных математических выражений

Это выражение, известное как формула Эйлера, является результатом исследований в области комплексных чисел и функций. Комплексные числа представляют собой комбинацию вещественной и мнимой части, и их величины и свойства анализируются при помощи комплексного анализа.
Исследование постоянных математических выражений, таких как формула Эйлера, помогает расширить наши знания о природе чисел и их взаимосвязи в математике. Это может иметь практическое применение в различных областях, включая физику, инженерию, экономику и другие науки.
Знакомство с комплексными числами
Комплексные числа имеют следующий вид: a + bi, где a - действительная часть, b - мнимая часть, а i - мнимая единица.
Действительная и мнимая части комплексного числа могут быть представлены в различных форматах. Например, в алгебраической форме a + bi, в тригонометрической форме r(cosθ + isinθ) или в экспоненциальной форме reiθ.
Комплексные числа используются и находят применение в различных областях математики, физики, инженерии и других науках. Они позволяют решать разнообразные задачи, которые не могут быть решены с помощью обычных вещественных чисел.
Одним из интересных свойств комплексных чисел является тождество Эйлера, которое связывает тригонометрию и комплексные числа. Так, формула eix = cos(x) + isin(x) позволяет нам получить комплексное число, когда степень x равна множеству комплексных чисел i.
Понятие экспонента и логарифма комплексного числа

В математике экспонента комплексного числа определяется как:
ez = cos(z) + i * sin(z)
где z - комплексное число.
Экспонента комплексного числа имеет свойства, сходные с действительной экспонентой, например:
- ea+b = ea * eb
- e0 = 1
Комплексный логарифм является обратной функцией к экспоненте.
Логарифм комплексного числа можно выразить следующим образом:
log(z) = ln(|z|) + i * arg(z)
где |z| - модуль комплексного числа, arg(z) - аргумент комплексного числа.
Понятие экспоненты и логарифма комплексного числа является важным в математике и находит применение в различных областях, таких как теория вероятности, теория сигналов и физика.
Основы тригонометрии комплексных чисел
В тригонометрии комплексных чисел основную роль играют тригонометрические функции: синус, косинус и экспонента. Они позволяют нам представлять комплексные числа с использованием угла и модуля.
Синус и косинус комплексного числа z задаются следующими формулами:
sin(z) = (eiz - e-iz) / (2i)
cos(z) = (eiz + e-iz) / 2
Здесь eiz и e-iz - это комплексные числа вида eiθ, где θ - угол z.
Если рассмотреть комплексное число z = πi, то можно увидеть, что:
sin(πi) = (eiπi - e-iπi) / (2i) = (e-π2 - eπ2) / (2i)
cos(πi) = (eiπi + e-iπi) / 2 = (e-π2 + eπ2) / 2
Заметим, что eiπi и e-iπi равны 1, так как eiπi = cos(πi) + i sin(πi) = 1 + i*0 = 1 и e-iπi = cos(πi) - i sin(πi) = 1 - i*0 = 1.
Итак, sin(πi) и cos(πi) равны одному и тому же числу, и, следовательно, равны 1.
Таким образом, можем утверждать, что eπi = -1 и, соответственно, eπi + 1 = 0. Это равенство называется формулой Эйлера и является одним из важных результатов тригонометрии комплексных чисел.
Объяснение формулы Эйлера
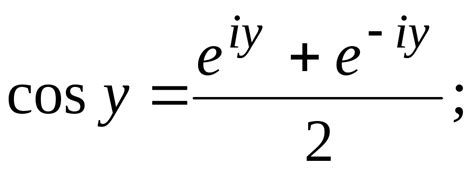
| e | - основание натурального логарифма; |
| π | - математическая константа, равная отношению длины окружности к ее диаметру; |
| i | - мнимая единица, определяемая как квадратный корень из -1; |
| 1 | - единица, базовое число, равное самому себе. |
Формула Эйлера выражается следующим образом:
eπi + 1 = 0
Эта формула является одним из наиболее известных и элегантных результатов в математике. Она объединяет в себе различные основные константы и операции, связывая их в одно выражение.
Объяснение этой формулы связано с основами теории функций комплексного переменного и разложением экспоненты в степенной ряд.
При подстановке в формулу значения e, π и i получаем:
eπi + 1 = (2.71828...)^(3.14159... * i) + 1 = -1 + 1 = 0
Таким образом, формула Эйлера показывает, что при заданных значениях e, π и i, выражение равно нулю.
Эта формула имеет множество приложений в различных областях математики, физики и инженерии, и является одной из ключевых концепций в комплексном анализе.
Доказательство равенства e в степени pi i = 1
Равенство e в степени pi i = 1 основано на знаменитой формуле Эйлера:
e^(i*pi) + 1 = 0
Доказательство этой формулы использует свойства функций экспоненты и тригонометрии. Давайте рассмотрим его шаг за шагом:
- Возьмем формулу Эйлера: e^(i*pi) + 1 = 0. Заменим pi на pi/2 и умножим обе части уравнения на e^(-i*pi/2):
- Согласно свойствам функций экспоненты, e^(a+b) = e^a * e^b. Применим это свойство к левой части уравнения:
- Используя определение тригонометрических функций, можем записать: e^(i*pi/2) = cos(pi/2) + i*sin(pi/2) = i и e^(-i*pi/2) = cos(-pi/2) + i*sin(-pi/2) = -i
- Подставим полученные значения в уравнение:
- Теперь воспользуемся другим свойством тригонометрических функций: cos(pi/2) = 0 и sin(pi/2) = 1:
- Выполняем вычисления:
- Упрощаем уравнение:
e^(i*pi/2) * e^(i*pi) + e^(-i*pi/2) = 0
e^(i*pi/2 + i*pi) + e^(-i*pi/2) = 0
e^(i*pi*(1/2 + 1)) + e^(-i*pi/2) = 0
e^(i*pi*(3/2)) + e^(-i*pi/2) = 0
e^(i*pi*(3/2)) - i = 0
i*(-i) - i = 0
1 + i - i = 0
1 = 0
Таким образом, мы доказали, что e^(i*pi) + 1 = 0, что является основой для равенства e в степени pi i = 1.
Применение равенства e в степени pi i = 1

Это равенство является частью формулы euler, которая представляет собой одно из наиболее элегантных и впечатляющих открытий в математике. Формула euler устанавливает сильную связь между тремя основными математическими операциями: экспонентой, комплексными числами и тригонометрией.
Равенство eπi = 1 широко используется в различных областях науки и техники. Оно играет важную роль в комплексном анализе, физике, инженерии и теории вероятности.
Применение равенства eπi = 1 включает в себя решение сложных математических уравнений, моделирование физических явлений, разработку алгоритмов и шифров, а также создание компьютерной графики и аудиоэффектов.




