Основной период функции является одним из основных понятий в математике, которое позволяет определить повторяющийся интервал значений функции. Он определяется как наименьшее положительное число T, для которого выполняется равенство f(x + T) = f(x) для всех значений x в области определения функции.
Таким образом, основной период указывает на это повторение функции и является важным инструментом для изучения периодических функций. Если найти основной период функции, то можно определить периодичность ее значений и использовать эту информацию для решения задач и проведения дальнейших исследований.
Для более наглядного понимания основного периода функции можно рассмотреть несколько примеров. Например, для функции синуса y = sin(x) основным периодом будет 2π, так как sin(x + 2π) = sin(x). Для функции косинуса y = cos(x) также основным периодом будет 2π, так как cos(x + 2π) = cos(x).
Исходное определение основного функционального периода
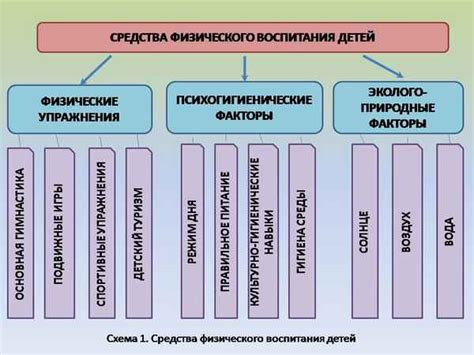
Пример 1:
- Рассмотрим функцию f(x) = sin(x).
- Ее область значений [-1, 1] является основным функциональным периодом.
- Это означает, что функция sin(x) принимает любое значение в интервале [-1, 1].
Пример 2:
- Рассмотрим функцию g(x) = 2x + 1.
- Ее основным функциональным периодом является (-∞, +∞), так как она определена на всей числовой прямой.
- Функция g(x) может принимать любое значение в этом интервале.
Основной функциональный период является важным понятием при изучении функций, так как он позволяет понять, как функция взаимодействует с разными значениями аргумента.
Основные характеристики функции
Основные характеристики функции включают:
- Область определения - это множество всех значений x, для которых функция определена.
- Область значений - это множество всех значений y, которые функция может принимать.
- График функции - это геометрическое представление функции на плоскости, где значения x откладываются по горизонтальной оси, а значения y - по вертикальной оси.
- Зависимость значений функции от аргументов - это связь, которая определяет, как каждому значению аргумента x соответствует значение функции y.
Знание основных характеристик функции помогает лучше понять ее свойства и использовать ее для решения математических задач.
Математическое определение основного периода функции

| Определение | Пример |
|---|---|
| Если для всех x в области определения функции f(x) выполняется равенство f(x) = f(x + T) | Если f(x) = f(x + 2π) для всех x в R, то основной период функции f(x) равен 2π. |
Основной период функции может быть положительным или отрицательным числом, в зависимости от поведения функции. На практике, основной период функции позволяет нам определить, как часто функция повторяет свои значения и выявить закономерности в ее поведении.
Пример: основной период синусоидальной функции
Синусоида - это график синусоидальной функции. Основной период синусоидальной функции - это наименьшее положительное число T, при котором функция f(x) повторяется снова и снова. Другими словами, это расстояние по оси x между двумя соседними повторениями графика функции.
Для функции f(x) = sin(x) основной период можно найти, используя свойства тригонометрии. Мы знаем, что sin(x) имеет период 2π, то есть функция повторяется через каждые 2π радиан. Таким образом, основной период функции f(x) = sin(x) равен 2π.
Давайте рассмотрим таблицу значений функции f(x) = sin(x) для нескольких значений аргумента x:
| Значение x | Значение f(x) = sin(x) |
|---|---|
| 0 | 0 |
| π/2 | 1 |
| π | 0 |
| 3π/2 | -1 |
| 2π | 0 |
Из таблицы видно, что значения функции f(x) = sin(x) повторяются через каждые 2π радиан, то есть через каждый основной период. График функции f(x) = sin(x) имеет форму синусоиды и повторяет себя с равными интервалами вдоль оси x.
Таким образом, в данном примере основной период синусоидальной функции f(x) = sin(x) равен 2π.
Периодическое поведение синуса и косинуса

Периодическими функциями являются синус и косинус, потому что они повторяются через один и тот же промежуток времени или пространства. Период, обозначаемый как Т, представляет собой время или расстояние, через которое функции повторяются. Для синуса и косинуса его значение составляет 2π.
Например, функция синуса, обозначаемая как sin(x), будет иметь период 2π. Это означает, что значения sin(x) будут повторяться каждые 2π единиц. Аналогично, функция косинуса, обозначаемая как cos(x), также будет иметь период 2π.
Периодическое поведение синуса и косинуса может быть полезно при решении задач из различных областей науки и математики. Например, в физике, когда мы анализируем колебания или волны, мы использовать синус и косинус для описания периодического поведения.
Таким образом, синус и косинус функции имеют периодическое поведение, которое повторяется через определенный промежуток времени или пространства. Использование периодического поведения синуса и косинуса широко распространено в науке и математике и имеет множество приложений.
Графическое представление основного периода
Рассмотрим график функции с заданным основным периодом - синусоиду. Основным периодом для синусоиды является $2\pi$, так как функция повторяется через каждые $2\pi$ радиан. График синусоиды описывает изменение значения функции в зависимости от изменения аргумента.
График синусоиды:  | График синусоиды с отмеченным основным периодом $2\pi$:  |
На графике синусоиды видно, что функция периодически повторяется с тем же графиком через каждые $2\pi$ радиан. Одна полная волна синусоиды занимает именно $2\pi$ радиан. Таким образом, основной период синусоиды составляет $2\pi$.
Графическое представление основного периода позволяет наглядно определить интервал, на котором функция имеет одинаковый характер изменения. Это полезно при анализе функций и решении задач, связанных с периодичностью и повторяемостью.
Пример: основной период линейной функции
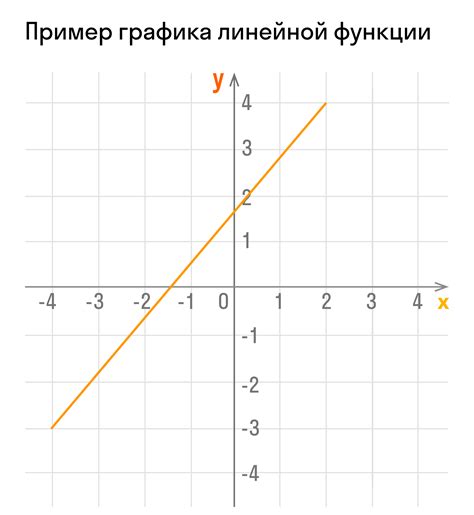
Рассмотрим функцию f(x) = 2x + 1 как пример линейной функции. Построим ее график:
На графике видно, что значение функции повторяется без изменения на всем интервале действительных чисел. Таким образом, основным периодом данной линейной функции является весь действительный интервал (-∞, +∞).
Как можно увидеть из данного примера, основной период линейной функции может быть достаточно простым и однозначным. Однако в более сложных функциях основной период может быть более узким и не совпадать с интервалом действительных чисел. В таких случаях можно использовать методы анализа графика функции и вычислении периода функции.
Отсутствие периодичности у линейной функции
Линейная функция не имеет периодов, так как ее график представляет собой прямую линию на координатной плоскости. Прямая линия не повторяется через определенные интервалы, а простирается на бесконечность.
Кроме того, линейная функция не имеет каких-либо точек симметрии или периодических повторений. Значения функции f(x) = ax + b изменяются линейно по мере изменения значения x. Таким образом, каждое значение x соответствует уникальному значению функции f(x).
Примером линейной функции без периодичности может служить функция f(x) = 2x + 3. Ее график будет представлять прямую линию, проходящую через точку (0, 3) и с угловым коэффициентом 2. Независимо от значения x, функция f(x) будет увеличиваться постоянно на 2.





