Круги Эйлера – это математическая концепция, которая имеет широкое применение в разных областях, начиная от графов и заканчивая компьютерными науками. Круг Эйлера – это графическая модель, которая используется для решения задач по поиску путей или циклов в графе.
Граф – это абстрактная структура, которая представляет собой набор вершин, соединенных ребрами. Поиск путей в графах может быть сложной задачей, особенно, если граф содержит множество вершин и ребер. Круги Эйлера помогают упростить эту задачу, предоставляя методику для нахождения путей и циклов в графе.
Важно отметить, что круги Эйлера применимы только к графам без ориентации, то есть графам, где ребра не имеют направления. Также, каждая вершина графа должна иметь четную степень, то есть количество инцидентных ей ребер должно быть четным числом (степенью вершины называется количество инцидентных ей ребер).
Что такое круги Эйлера?
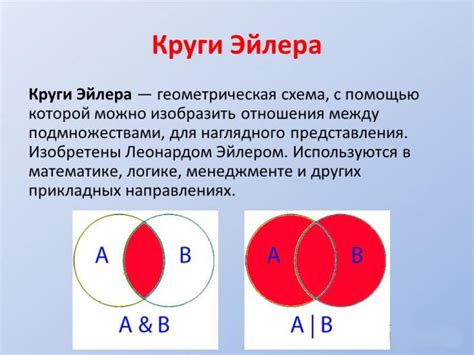
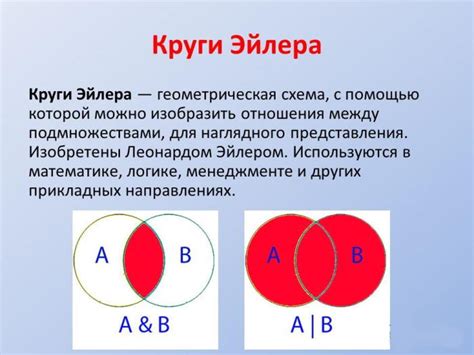
Круги Эйлера представляют собой эллипсы или окружности, которые пересекаются в различных комбинациях, формируя области пересечения. Каждая область пересечения отражает совпадение элементов между двумя или более наборами. Чем больше область пересечения, тем больше элементов общих для этих наборов.
Круги Эйлера широко используются в различных областях знаний, таких как математика, логика, статистика, информатика и даже визуализация данных. Они позволяют наглядно представить, например, количество общих элементов между разными группами данных или содержимым различных категорий.
Создание кругов Эйлера включает в себя определение наборов элементов и определение их пересечений. Затем можно использовать специальные программы или инструменты для визуализации кругов Эйлера, которые автоматически генерируют графическое представление.
Описание и применение
Круги Эйлера широко применяются в практических областях, таких как статистика, логика, биология и информатика. Они помогают визуализировать сложные отношения между различными группами или категориями и понять, какие элементы являются общими для двух или более множеств.
Например, в статистике круги Эйлера могут быть использованы для иллюстрации пересечений в данных. Представление в виде кругов Эйлера помогает исследователям определить, какие факторы связаны с определенными явлениями или событиями.
В информатике круги Эйлера используются для моделирования логических отношений между объектами или понятиями. Они могут помочь организовать информацию и определить, какие элементы имеют одинаковые характеристики или связи.
Целью использования кругов Эйлера является облегчение понимания сложных взаимоотношений и организации информации. Они позволяют визуализировать данные и выявить общие или уникальные элементы множеств. Круги Эйлера могут быть особенно полезны при анализе больших объемов данных или при работе с комплексными моделями.
Как решать круги Эйлера?
Для решения кругов Эйлера необходимо использовать методы комбинаторики и алгоритмы, которые позволяют найти все возможные комбинации и перестановки элементов. Вот основные шаги для решения кругов Эйлера:
- Изучите задачу и определите, какие элементы присутствуют в круге и как они связаны друг с другом.
- Составьте список элементов и определите, какие из них являются начальными пунктами, а какие - конечными.
- Используя алгоритмы комбинаторики, создайте все возможные комбинации элементов и запишите их в таблицу.
- Проверьте каждую комбинацию на соответствие условиям задачи и отметьте те, которые удовлетворяют критериям круга Эйлера.
- Определите, является ли задача согласованной - то есть, может ли быть построен круг Эйлера. Если нет, то решение невозможно.
- Выберите оптимальный вариант круга Эйлера из полученных комбинаций. Если таких вариантов несколько, выберите тот, который удовлетворяет дополнительным критериям (например, минимальное количество переходов).
Если вы последуете этим шагам и проведете детальный анализ каждого элемента, то сможете успешно решить задачу о кругах Эйлера.
Примеры и задачи
Пример 1:
Рассмотрим граф с вершинами A, B, C и ребрами AB, AC и BC. Найдем количество различных путей длины 2.
Для этого воспользуемся матрицей смежности графа:
Матрица смежности:
A B C
A 0 1 1
B 1 0 1
C 1 1 0
В матрице смежности на пересечении строки A и столбца B стоит 1, что означает наличие ребра между вершинами A и B. Таким образом, существует 1 путь длины 1 между вершинами A и B. Также существуют пути длины 1 между вершинами A и C, и между вершинами B и C.
Для нахождения путей длины 2, умножим матрицу смежности саму на себя:
A B C
A 0 1 1
B 1 0 1
C 1 1 0
Умножив матрицу смежности на саму себя, получаем следующую матрицу:
Матрица A^2:
A B C
A 2 1 1
B 1 2 1
C 1 1 2
В матрице A^2 на пересечении строки A и столбца B стоит 1, что означает наличие пути длины 2 между вершинами A и B. Аналогично, существуют пути длины 2 между вершинами A и C, и между вершинами B и C.
Таким образом, ответ на задачу равен 3.
Пример 2:
Рассмотрим граф с вершинами A, B, C, D и ребрами AB, AC, AD и BC. Найдем количество различных путей длины 3.
Для этого воспользуемся матрицей смежности графа:
Матрица смежности:
A B C D
A 0 1 1 1
B 1 0 1 0
C 1 1 0 0
D 1 0 0 0
Для нахождения путей длины 3, умножим матрицу смежности саму на себя два раза:
A B C D
A 0 1 1 1
B 1 0 1 0
C 1 1 0 0
D 1 0 0 0
Матрица A^2:
A B C D
A 3 1 1 0
B 1 2 1 0
C 1 1 2 0
D 1 0 0 1
Матрица A^3:
A B C D
A 5 2 2 0
B 2 3 2 0
C 2 2 3 0
D 2 0 0 1
В матрице A^3 на пересечении строки A и столбца B стоит 2, что означает наличие 2 путей длины 3 между вершинами A и B. Аналогично, существуют 2 пути длины 3 между вершинами A и C, 2 пути длины 3 между вершинами A и D, 3 пути длины 3 между вершинами B и C, и 1 путь длины 3 между вершинами B и D.
Таким образом, ответ на задачу равен 10.




