Теория равенства является одной из основных тем логики и математики. Концепция тождественной равности находит применение во многих областях знания, прежде всего в алгебре и математической логике. Суть тождественной равности заключается в том, что два выражения или объекта считаются равными, если они обладают одинаковыми свойствами и действиями.
Существуют определенные свойства действий, которые подтверждают тождественную равность. Одним из таких свойств является свойство рефлексивности. Оно формулируется так: любой объект или выражение равно самому себе. Это свойство основополагающее и лежит в основе всех других свойств равенства.
Важным свойством действий, подтверждающим тождественную равность, является свойство симметрии. Оно означает, что если два объекта или выражения равны между собой, то они равны и при обратной замене местами. Другими словами, если A=B, то B=A.
Еще одним важным свойством является свойство транзитивности. Это свойство говорит о том, что если A=B и B=C, то A=C. Оно позволяет установить равенство между тремя объектами или выражениями на основе уже известного равенства двух из них.
Как доказать тождественную равность действий?
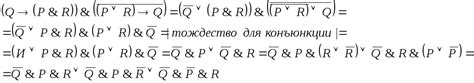
Для доказательства тождественной равности действий необходимо привести убедительные аргументы и логические выкладки. Все свойства действий, подтверждающие тождественную равность, должны быть строго доказаны и обоснованы.
Одним из основных методов, позволяющих доказывать тождественную равность действий, является использование алгебраических преобразований и уравнений. Путем последовательного применения преобразований и решения уравнений можно убедиться в равенстве действий.
Также важным фактором является использование значений переменных и фиксированных условий, чтобы подтвердить равность действий в конкретных ситуациях. Использование численных примеров и конкретных значений позволяет более наглядно демонстрировать тождественную равность.
Некоторые действия могут быть равными не всегда и не во всех условиях. В таких случаях необходимо указать ограничения и условия, при которых данная тождественная равность выполняется.
Таким образом, для доказательства тождественной равности действий необходимо использовать алгебраические методы, логические выкладки, а также конкретные численные примеры и условия. Только строгое и убедительное доказательство позволяет установить тождественную равность действий.
Установление равенства с помощью свойства ассоциативности
Для установления равенства с помощью свойства ассоциативности, необходимо выполнить следующие шаги:
- Разложить выражение на группы, где каждая группа содержит операции, имеющие одинаковый приоритет.
- После разложения, перегруппировать выражение, перемещая группы вокруг операндов и операций так, чтобы порядок выполнения операций не изменился, но порядок скобок был изменен.
- Сравнить новое выражение с исходным выражением, применяя правила сокращения и раскрытия скобок. Если новое выражение эквивалентно исходному, то можно установить равенство.
Например, пусть дано выражение (2 + 3) + 4. С помощью свойства ассоциативности, можно перегруппировать скобки и записать выражение как 2 + (3 + 4). Затем, применяя правило сложения, получим равенство 2 + 7 = 9, что подтверждает тождественную равность исходного выражения.
Свойство ассоциативности широко применяется в математике и программировании для упрощения выражений и работы с большими объемами данных. Правильное использование этого свойства позволяет существенно сократить объем вычислений и повысить эффективность решений задач.
Демонстрация тождества с использованием свойства коммутативности
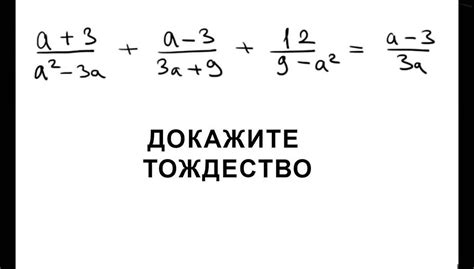
Для демонстрации тождественной равности с использованием свойства коммутативности рассмотрим пример сложения чисел:
Дано: a = 5, b = 3
Тождество: a + b = b + a
Тождественную равность можно проиллюстрировать следующим образом:
- Сложим числа по порядку: a + b = 5 + 3 = 8
- Сложим числа в обратном порядке: b + a = 3 + 5 = 8
- Получаем одинаковый результат, что подтверждает тождественную равность a + b = b + a
Свойство коммутативности помогает упростить вычисления и проводить операции независимо от порядка элементов, что является важным в математике и алгебре.
Проверка равенства с использованием свойства дистрибутивности
Для примера, рассмотрим следующее выражение:
a * (b + c) = a * b + a * c
Это выражение описывает свойство дистрибутивности для умножения и сложения. Оно говорит нам о том, что при умножении числа a на сумму чисел b + c, мы можем распределить это умножение на оба слагаемых, и результат будет равен сумме умноженных чисел. Например, если a = 2, b = 3 и c = 4, то:
2 * (3 + 4) = 2 * 3 + 2 * 4
2 * 7 = 6 + 8
14 = 14
Таким образом, свойство дистрибутивности позволяет нам упрощать и проверять равенство выражений, с помощью перестановки и объединения операций.
Проверка равенства с использованием свойства дистрибутивности является важным инструментом в алгебре, который позволяет упрощать и решать различные математические задачи.
Применение свойства обращения для доказательства равенства действий

Применимость свойства обращения исключительно в тех случаях, когда обратное действие существует и является допустимым. Например, для действий сложения и вычитания, обращение будет вычитание и сложение соответственно.
Рассмотрим простой пример применения свойства обращения. Пусть имеется действие сложения: $a + b$, где $a$ и $b$ - произвольные числа. Применяя свойство обращения, мы можем предположить, что обратное действие - это вычитание. То есть, если мы выполним сложение и затем вычтем из этого результата $b$, то должны получить исходное значение $a$.
То есть:
$(a + b) - b = a$
Таким образом, мы доказали равенство действий сложения и вычитания с помощью свойства обращения.




