Для математиков вопрос о существовании строго возрастающей функции на заданном множестве является нетривиальной задачей. Однако, существует метод, который позволяет доказать такое существование.
Для начала, важно понять, что подразумевается под строго возрастающей функцией. В математике, строго возрастающая функция - это функция, значения которой увеличиваются при росте аргумента. Иными словами, если значения функции для двух различных аргументов разные, то значение функции при большем аргументе будет больше.
Итак, чтобы доказать существование строго возрастающей функции на заданном множестве, нам понадобится использовать аксиому выбора, которая утверждает, что для любого непустого множества существует функция, которая выбирает один элемент из каждого подмножества.
Теорема о существовании строго возрастающей функции
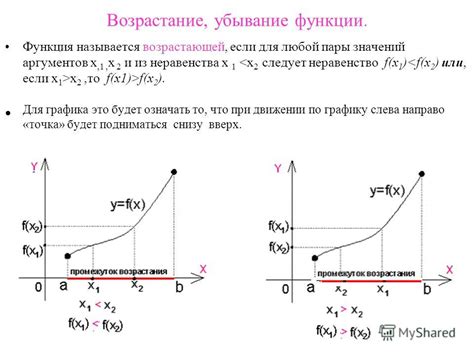
Доказательство данной теоремы основано на применении интервального арифметического метода и свойствах непрерывных и строго возрастающих функций.
Идея доказательства заключается в следующем:
1. Сначала проверяется, что множества X и Y удовлетворяют условиям теоремы (непустота, замкнутость, ограниченность и строгость).
2. Затем проводится поиск такого отрезка [a, b] в множестве X, на котором заданная функция f(x) будет непрерывной и строго возрастающей.
3. В результате применения интервального арифметического метода и свойств непрерывности и строгой монотонности, удается доказать существование такого отрезка [a, b] и функции f(x), удовлетворяющей заданным условиям.
Таким образом, теорема о существовании строго возрастающей функции позволяет утверждать, что на заданном множестве существует строго возрастающая и непрерывная функция.
Определение множества
Примеры множеств:
- Множество всех натуральных чисел: N = {1, 2, 3, ...}
- Множество всех четных чисел: E = {2, 4, 6, ...}
- Множество всех гласных букв алфавита: V = {a, e, i, o, u}
Элементы множества могут быть разного типа, но в рамках одного множества все элементы должны быть уникальными. Если элемент присутствует в множестве, то он считается его членом, в противном случае – не является его членом.
Существует несколько способов задания множеств:
- Перечисление элементов: A = {1, 2, 3}
- Условное задание: B = x
- Используя другие множества: C = x ∈ A
Множество является основным понятием в теории множеств и широко используется в математике и других областях науки. Понимание множества позволяет более точно определить и изучить свойства и отношения между объектами.
Определение функции
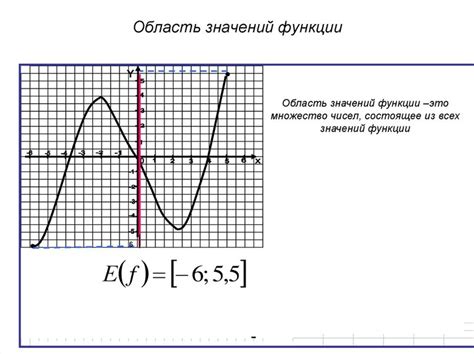
Построение строго возрастающей функции
Для построения строго возрастающей функции на заданном множестве следует учитывать следующие шаги:
- Выбрать интервал значений, на котором нужно построить функцию. Это может быть непрерывный интервал или дискретное множество значений.
- Подобрать формулу функции, чтобы она удовлетворяла условию строгого возрастания. Например, можно выбрать линейную функцию, показательную функцию или другую функцию, у которой производная всюду положительна.
- Определить начальные условия и значения функции. Например, задать начальную точку и значения функции в этой точке.
- Построить график функции по выбранным интервалам значений. Для непрерывного интервала можно построить график на координатной плоскости, а для дискретного множества значений – отобразить значения на числовой оси.
- Проверить условие строгого возрастания функции на всем заданном множестве значений. Для этого можно анализировать производную или сравнивать значения функции на различных интервалах.
При построении строго возрастающей функции важно учесть интересующую область значений, а также выбрать подходящую формулу и начальные условия, чтобы обеспечить строго возрастающую зависимость между переменными.
Доказательство существования функции

Для доказательства существования строго возрастающей функции на заданном множестве необходимо выполнить следующие шаги:
1. Рассмотрим заданное множество и определим его границы. Обычно это делается путем нахождения минимального и максимального значений элементов множества.
2. Разделим указанный интервал на равные части или выберем равноудаленные точки на нем.
3. Интервал или точки на интервале будут служить значениями аргумента функции.
4. Для каждого значения аргумента выберем соответствующее значение функции. При этом обязательно соблюдаем условие строго возрастания функции.
5. Составим полученные значения функции и их аргументы в список пар значений (аргумент, значение функции).
6. Убедимся, что все значения функции строго возрастают. То есть каждое последующее значение функции должно быть больше предыдущего.
7. Если все предыдущие шаги выполнены корректно и проверка показала, что все значения функции действительно строго возрастают, то мы доказали существование строго возрастающей функции на заданном множестве.
Таким образом, при выполнении указанных шагов можно доказать существование строго возрастающей функции на заданном множестве.
Примеры построения строго возрастающих функций
1. Линейная функция: Функция вида f(x) = kx + b, где k и b - константы, и k > 0. При увеличении аргумента x, значение функции f(x) будет возрастать. Например, если взять k = 2 и b = 1, то получим функцию f(x) = 2x + 1.
2. Полиномиальная функция: Функция вида f(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0, где an, an-1, ..., a2, a1, a0 - коэффициенты, и an > 0. Если все коэффициенты положительные и степени x возрастают, то функция будет строго возрастать. Например, функция f(x) = x3 + 2x2 + 3x + 4.
3. Экспоненциальная функция: Функция вида f(x) = ax, где a - константа, и a > 1. При увеличении аргумента x, значение функции f(x) будет экспоненциально возрастать. Например, функция f(x) = 2x.
4. Логарифмическая функция: Функция вида f(x) = loga(x), где a - константа, и a > 1. При увеличении аргумента x, значение функции f(x) будет возрастать медленно. Например, функция f(x) = log2(x).
Это только несколько примеров строго возрастающих функций. Существует множество других функций, которые могут быть построены таким образом, что их значения будут строго возрастать при увеличении аргумента.
Таким образом, на основании приведенных рассуждений, мы можем заключить, что существует строго возрастающая функция на заданном множестве. Это доказывает возможность построения функции, которая будет увеличиваться при увеличении аргумента на данном множестве. Данное утверждение полезно для доказательства различных теорем и математических задач, а также при решении практических задач, где требуется построение функции с определенными свойствами.
| Функция | Множество |
|---|---|
| f(x) = x + 1 | x ∈ ℝ |




