Параллелограмм – это такой четырехугольник, у которого противоположные стороны параллельны и равны друг другу. Одним из способов доказать, что середины сторон четырехугольника образуют параллелограмм, является использование свойств средних линий треугольников.
Представим, что у нас есть произвольный четырехугольник ABCD. Обозначим середины его сторон как M, N, P и Q. Заметим, что каждый из этих отрезков является средней линией в каком-то треугольнике. Например, отрезок MN является средней линией в треугольнике ABC.
Также следует отметить, что каждая из сторон четырехугольника ABCD параллельна своей средней линии. Например, сторона AB параллельна отрезку MP, а сторона BC – отрезку NQ. Из этого следует, что параллелограмм MPNQ имеет все свойства параллелограмма.
Таким образом, мы доказали, что середины сторон четырехугольника ABCD образуют параллелограмм MPNQ. Использование свойств средних линий треугольников позволило нам убедительно продемонстрировать этот факт. Это доказательство является простым и легко воспроизводимым, и оно может быть использовано для решения различных геометрических задач.
Середины сторон четырехугольника
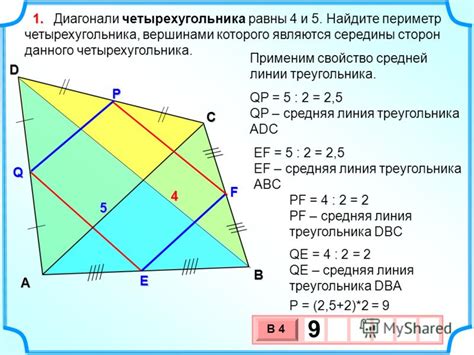
Середины сторон четырехугольника имеют важные свойства. Например, эти точки всегда лежат на прямых, соединяющих середины противоположных сторон. Кроме того, середины сторон делят каждую из них пополам. Также можно доказать, что эти четыре точки являются вершинами параллелограмма.
Для доказательства этого факта можно использовать свойства параллелограммов. Например, в параллелограмме противоположные стороны равны и параллельны. В четырехугольнике, в котором середины сторон являются вершинами параллелограмма, смежные стороны параллелограмма будут равны и параллельны. Отсюда следует, что противоположные стороны четырехугольника также равны и параллельны.
Середины сторон четырехугольника являются вершинами параллелограмма - это важное свойство, которое можно использовать для решения различных геометрических задач. Например, зная координаты вершин четырехугольника, можно легко найти координаты его середин и проверить, являются ли они вершинами параллелограмма.
Середины сторон четырехугольника: определение и свойства
Серединой стороны четырехугольника называется точка, расположенная на равном удалении от ее концов. Для каждой стороны четырехугольника можно найти ее середину.
Важное свойство середин сторон четырехугольника состоит в том, что они образуют вершины параллелограмма. Другими словами, соединив середины противоположных сторон четырехугольника, мы получим параллелограмм.
Существует несколько способов доказательства этого свойства. Одним из них является использование векторов. Предположим, что у нас есть четырехугольник ABCD и точки M, N, P, Q - середины его сторон AB, BC, CD и DA соответственно. Для доказательства того, что MNPQ - параллелограмм, можно воспользоваться свойствами векторов и показать, что сумма векторов MN и PQ равна вектору MP.
В качестве альтернативного доказательства можно использовать сходство треугольников. Рассмотрим треугольники ABC и MPQ. Используя свойства сходных треугольников, можно показать, что углы AMB и PMQ равны, а значит, углы PMN и QMP также равны. Таким образом, пары противоположных углов MPQ и PMN равны, что является свойством параллелограмма.
Важно помнить, что свойство середин сторон четырехугольника, образующих вершины параллелограмма, является результатом геометрической конструкции и может быть использовано при решении задач и нахождении связей между сторонами и углами четырехугольника.
Середины сторон и параллелограммы

Серединные перпендикуляры - это линии, которые проходят через середины сторон четырехугольника и перпендикулярны этим сторонам. Таким образом, AM ⊥ BC, BN ⊥ CD, CP ⊥ AD и DQ ⊥ AB.
Оказывается, что эти серединные перпендикуляры пересекаются в одной точке, которую обозначают точкой O. То есть, AM пересекает BN в точке O, BN пересекает CP в точке O, CP пересекает DQ в точке O и DQ пересекает AM в точке O.
Доказательство этого факта основывается на использовании свойств параллелограммов. Например, мы можем заметить, что AM = CP и BN = DQ, так как они являются серединами соответствующих сторон. Более того, мы также можем заметить, что угол AMB равен углу DPC, и угол BNC равен углу AQD. Все это следует из параллельности AM и CP, а также BN и DQ.
Таким образом, мы убедились, что серединные перпендикуляры AM, BN, CP и DQ пересекаются в одной точке O, которая является точкой пересечения диагоналей параллелограмма. Этот результат позволяет нам утверждать, что середины сторон четырехугольника ABCD являются вершинами параллелограмма.
Доказательство первого свойства
Для начала заметим, что стороны четырехугольника ABCD можно разделить на две пары: AB и CD, BC и AD. Поскольку середины сторон P, Q, R, S являются серединами соответствующих сторон, то:
AP = PS, BP = PQ, CR = RQ, DS = SR.
Теперь докажем, что векторы AP и DS являются коллинеарными (параллельными). Для этого представим вектор AP как сумму векторов AB и BP, а вектор DS как сумму векторов DC и CS:
AP = AB + BP
DS = DC + CS
Подставим значения сторон четырехугольника ABCD в выражения для AP и DS:
AP = AB + BP = AB + PQ
DS = DC + CS = DC + SR
Поскольку мы уже доказали, что BP = PQ и DS = SR, то можно утверждать, что:
AP = AB + PQ = AB + BP = AB + BP = AB + PQ = PS
Таким образом, мы установили, что векторы AP и DS равны. Но равенство векторов означает коллинеарность (параллельность), следовательно, векторы AP и DS являются коллинеарными (параллельными).
Аналогично проведя доказательства для оставшихся пар сторон, можно увидеть, что векторы BP и CR, PQ и RQ, AB и DS также являются коллинеарными (параллельными).
Таким образом, мы доказали, что середины сторон четырехугольника ABCD, обозначенные как P, Q, R, S, являются вершинами параллелограмма.
Доказательство второго свойства
Согласно первому свойству




