Комплексные числа являются мощным инструментом математики, позволяющим работать с величинами, в которых присутствует не только действительная, но и мнимая составляющая. Таким образом, они представляют собой числа вида z = a + bi, где a и b - действительные числа, а i - мнимая единица, квадрат которой равен -1.
Одним из способов представления комплексных чисел является тригонометрическая форма. В этой форме число z представляется в виде z = |z|(cosθ + isinθ), где |z| - модуль числа z, а θ - аргумент числа z. Модуль |z| определяется как расстояние между точкой, соответствующей комплексному числу z, и началом координат в комплексной плоскости.
Аргумент θ определяется как угол между положительным направлением вещественной оси и радиус-вектором, соединяющим начало координат и точку, соответствующую комплексному числу z. Аргумент определяется с точностью до добавления или вычитания 2πk, где k - целое число.
Тригонометрическая форма комплексного числа z позволяет упростить выполнение операций над комплексными числами, таких как сложение, вычитание и умножение. Кроме того, она находит широкое применение в различных областях науки и техники, включая электротехнику, физику и инженерию.
Определение тригонометрической формы

Комплексное число z в тригонометрической форме может быть записано в виде z = r · (cos(θ) + i sin(θ)), где:
- r - модуль комплексного числа, равный расстоянию от начала координат до точки, представленной комплексным числом;
- θ - аргумент комплексного числа, который является углом между положительным направлением вещественной оси и отрезком, соединяющим начало координат и точку, представляющую комплексное число.
Модуль и аргумент комплексного числа могут быть легко определены с помощью формул:
- r = |z| = sqrt(x2 + y2), где x - действительная часть комплексного числа, а y - мнимая часть комплексного числа;
- θ = arg(z) = tan-1(y/x), где x и y - действительная и мнимая части комплексного числа соответственно.
Тригонометрическая форма комплексного числа удобна для выполнения операций с комплексными числами, таких как умножение, деление и возведение в степень.
Комплексное число и его представление
Действительная часть комплексного числа обозначается Re(z) и представляет собой обычное действительное число. Мнимая часть обозначается Im(z) и умножается на мнимую единицу i.
Комплексное число можно представить в разных формах. Одна из них - тригонометрическая форма. В тригонометрической форме комплексное число представляется в виде модуля и аргумента.
Модуль комплексного числа обозначается |z| и определяется как расстояние от начала координат до точки, которая соответствует комплексному числу на комплексной плоскости.
Аргумент комплексного числа обозначается arg(z) и определяется как угол между положительным направлением действительной оси и лучом, идущим от начала координат до точки, соответствующей данному комплексному числу.
Тригонометрическая форма комплексного числа z выглядит следующим образом: z = |z| * exp(i * arg(z)), где exp(i * arg(z)) - экспонента, равная cos(arg(z)) + i * sin(arg(z)).
Таким образом, тригонометрическая форма комплексного числа позволяет представлять его в виде модуля и аргумента, что удобно при решении задач, связанных с операциями над комплексными числами.
Модуль комплексного числа и его связь с тригонометрической формой

Модуль комплексного числа z обозначается как |z| и представляет собой расстояние от начала координат до точки, соответствующей комплексному числу z на комплексной плоскости. Модуль числа z можно найти по формуле:
|z| = √(Re(z)^2 + Im(z)^2)
где Re(z) - действительная часть комплексного числа, Im(z) - мнимая часть комплексного числа.
Связь модуля комплексного числа с его тригонометрической формой выражается через теорему Пифагора прямоугольного треугольника на комплексной плоскости. Комплексное число z можно представить в виде:
z = |z| * (cos(θ) + i*sin(θ))
где |z| - модуль комплексного числа, θ - аргумент комплексного числа, cos(θ) - косинус аргумента, sin(θ) - синус аргумента.
Таким образом, модуль комплексного числа позволяет нам определить его расстояние от начала координат, а его тригонометрическая форма представляет числовое значение и угол для комплексного числа на комплексной плоскости.
Аргумент комплексного числа и его значение в тригонометрической форме
Значение аргумента комплексного числа в тригонометрической форме выражается через функцию арктангенс. Пусть z = a + bi, где a представляет собой вещественную часть числа, а b - мнимую. Тогда аргумент числа z можно найти по формуле:
Arg(z) = arctg(b/a)
Значение аргумента определено с точностью до добавления или вычитания кратного числа 2π:
Arg(z + 2πk) = Arg(z), где k - целое число.
Значение аргумента комплексного числа в тригонометрической форме можно записать как:
z = |z| * (cos(Arg(z)) + i * sin(Arg(z)))
Здесь |z| - модуль комплексного числа, а cos(Arg(z)) и sin(Arg(z)) - косинус и синус аргумента соответственно.
Тригонометрическая форма позволяет удобно представлять комплексные числа и выполнять с ними арифметические операции. Она также связана с полярным представлением чисел на комплексной плоскости.
Преобразование алгебраической формы в тригонометрическую форму
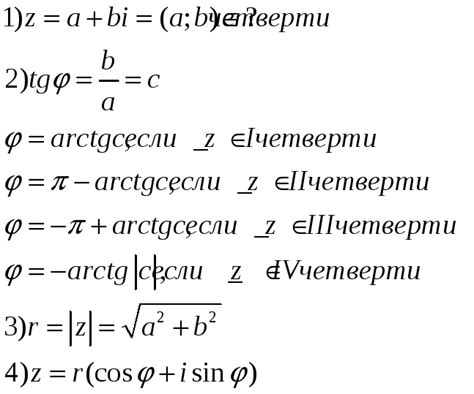
Для преобразования комплексного числа из алгебраической формы в тригонометрическую форму необходимо найти его модуль и аргумент.
- Найдем модуль комплексного числа z по формуле |z| = √(Re(z)^2 + Im(z)^2), где Re(z) - действительная часть числа z, Im(z) - мнимая часть числа z.
- Найдем аргумент комплексного числа z по формуле θ = arctg(Im(z)/Re(z)), где arctg - арктангенс.
После нахождения модуля и аргумента комплексного числа, его тригонометрическая форма может быть записана как z = r(cosθ + isinθ).
Преобразование алгебраической формы в тригонометрическую форму позволяет удобно представить комплексное число в плоскости (декартова плоскость), где модуль числа является расстоянием от начала координат до точки, а аргумент представляет угол между положительным направлением оси x и направлением от начала координат до точки числа.
Преобразование тригонометрической формы в алгебраическую форму
Тригонометрическая форма записи комплексного числа представляет его в виде суммы или разности между двумя тригонометрическими функциями. Она имеет следующий вид:
z = r(cosθ + isinθ)
где r - модуль комплексного числа, а θ - Аргумент, выраженный в радианах.
Для преобразования тригонометрической формы в алгебраическую форму комплексного числа необходимо использовать формулы Эйлера.
Формулы Эйлера позволяют выразить косинус и синус через экспоненциальную функцию:
eiθ = cosθ +isinθ
Применяя формулы Эйлера к тригонометрической форме комплексного числа, получаем:
z = r(eiθ)
Далее, используя свойства экспоненты, приводим выражение к следующему виду:
z = reiθ = r(cosθ + isinθ)
Таким образом, мы получаем алгебраическую форму записи комплексного числа, где модуль числа указывается перед экспоненциальной формой, а тригонометрические функции выражены через косинус и синус.
Преобразование из тригонометрической формы в алгебраическую форму позволяет упростить вычисления с комплексными числами, так как алгебраическая форма удобнее для выполнения операций сложения, вычитания, умножения и деления.




